

ID 02966
Techniky luštění klasického sudoku
Celý následující přehled je pro vás připraven také zde ve formě PDF souboru, který si můžete prohlédnout nebo pomocí pravého tlačítka myši a volbou Uložit cíl jako ... stáhnout a vytisknout.
Obsah:
1. Základní pojmy
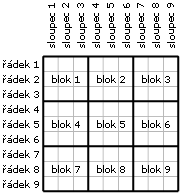
Sudoku hlavolam (puzzle) obsahuje celkem 81 buněk (cells), devět vodorovných řádků (rows), devět svislých sloupců (columns) a devět skupin po 3×3 buňkách nazývaných bloky (blocks) nebo boxy (boxes). Řádky, sloupce a bloky jsou počítány dle obrázku vlevo.
Pokud uvádíme jednotlivé buňky v řádku, počítáme je zleva doprava, pokud ve sloupci, potom shora dolů. Jestliže uvádíme buňky v jednom bloku, počítáme je podobně jako bloky v celém hlavolamu, tedy po řádcích.
V některých případech je potřeba uvést buňku pomocí jejích souřadnic. Souřadnice se vyjadřuje ve formátu RXCY, což znamená řádek (row) X, sloupec (column) Y. X a Y samozřejmě vyjadřuje číslici 1 až 9.
Všechny číslice, které v určité chvíli připadají v úvahu, že by mohly patřit do určité buňky, se nazývají kandidáti buňky (cell's candidates). Luštitelé sudoku si většinou, zejména u obtížnějších úloh, vpisují kandidáty do buněk (na papíře tužkou, v on-line formuláři do spec. kolonek na okraji buňky (u nás na sudoku.na-webu.cz u horního okraje buňky)).
2. Techniky odkrývání buněk
Existuje několik technik jak zjistit obsah buňky. Tady je přehled některých z nich. Techniky mají své zaužívané anglické označení, které budeme používat. Toto označení považujeme za název techniky a proto je většinou nepřekládáme.
Základní techniky pro vepsání kandidáta do buňky
Pomocí následujících dvou technik můžeme přímo zapsat do buňky výslednou číslici.
2.1 Technika Naked Single
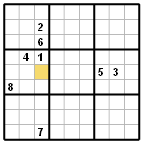
Tuto techniku můžeme také nazvat "jediný kandidát" (sole candidate).
Často je možné do určité buňky zapsat jen jednu určitou číslici, neboť všechny ostatní jsou vyloučeny díky již zapsaným číslicím v příslušném sloupci, řádku a bloku.
Na obrázku je příklad, kde do označené buňky je možno zapsat pouze číslici 9 (čili pro onu buňku existuje pouze jediný kandidát).
Tato technika je většinou postačující pro luštění těch nejlehčích sudoku hlavolamů.
2.2 Technika Hidden Single
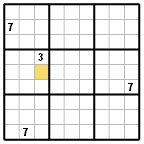
Tuto techniku můžeme také nazvat "ojedinělý kandidát" (unique candidate).
Pokud v určitém sloupci, řádku nebo bloku existuje pouze jedna buňka, ve které je kandidátem určitá číslice, pak je jasné, že tato číslice musí být právě v oné buňce.
V příkladu na obrázku je označená buňka jedinou ve třetím sloupci, kde je kandidátem (nemusí být jediným) číslice 7. Proto musí být v označené buňce číslice 7.
Další techniky pro redukci počtu kandidátů v buňkách
Následující techniky mají za úkol pouze redukovat počet kandidátů v buňkách tak, aby bylo možno následně aplikovat některou z výše popsaných technik Naked Single nebo Hidden Single.
2.3 Technika interakce bloku a sloupce / řádku (Block and Column / Row Interactions)
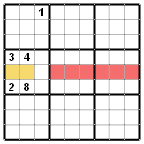
V některých případech je ze situace v bloku a jeho okolí jasné, že se kandidáti určitého čísla nacházejí v daném bloku pouze v jednom řádku nebo pouze v jednom sloupci. Pak se dají vyloučit kandidáti onoho čísla ve zbytku řádku (sloupce) tedy v sousedních blocích.
Nejlépe to osvětlí příklad. Ze situace v obrázku je patrno, že číslice 1 se v bloku 4 může vyskytovat pouze v jednom ze dvou žlutě vyznačených polí a tedy pouze v řádku 5. Proto je možné ve zbytku řádku 5 (v růžově označených buňkách) zredukovat kandidáty a vyloučit z nich číslici 1.
2.4 Technika interakce bloku a bloku (Block / Block Interactions)
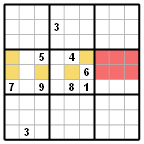
Pokud ve dvou sousedních blocích leží všichni kandidáti stejné číslice pouze ve dvou řádcích či sloupcích, můžeme ve třetím sousedním bloku kandidáty této číslice v oněch dvou řádcích či sloupcích vyloučit.
Příklad - na obrázku se nacházejí kandidáti číslice 3 v blocích 4 a 5 pouze v buňkách označených žlutě (tedy pouze ve dvou řádcích). Protože v každém bloku musí být číslice 3 v jednom z těchto dvou řádků, je možné ve třetím sousedním bloku v růžových buňkách eliminovat kandidáty číslice 3 (nebo-li číslice 3 se může nacházet pouze v nerůžových buňkách onoho bloku).
2.5 Technika Naked Subset
Tato technika se nazývá také Naked Pair pokud pracujeme se dvěma číslicemi jako kandidáty, popř. Naked Triplet, pracujeme-li se třemi číslicemi nebo Naked Quad pro čtyři. Pro větší počet číslic jako kandidátů se tato metoda prakticky nevyskytuje.
Obecné pravidlo této techniky říká - "Pokud počet různých kandidátů v některých buňkách jednoho řádku, sloupce nebo bloku je stejný jako počet těchto buněk, pak je možné tyto kandidáty z ostatních buněk onoho řádku, sloupce nebo bloku eliminovat." Zní to na první pohled dost odpudivě, ale není to nic složitého. Pokud toto pravidlo uvedu pro Naked Pair, zní takto: "Pokud se ve dvou buňkách jednoho řádku, sloupce nebo bloku nacházejí pouze dva různí kandidáti, můžeme tyto kandidáty z ostatních buněk onoho řádku, sloupce nebo bloku odstranit." Podobně pro Naked Triplet a Naked Quad.
Příklad s obrázkem ukazuje postupné eliminování kandidátů.

V řádku na prvním obrázku jsou zapsaní všichni kandidáti, v jedné buňce již je přímo konečná číslice 5. Z obrázku je patrno, že v první a osmé buňce se nacházejí pouze dva kandidáti - 6 a 7. Tyto dvě číslice tedy patří do oněch dvou buněk (nevíme která do které). Z ostatních buněk v řádku tedy můžeme kandidáty 6 a 7 zrušit.

To ale není vše, touto metodou můžeme v tomto případě i pokračovat dál, neboť zrušením kandidátů 6 a 7 se v sedmé a deváté buňce objevila nová dvojice jediných kandidátů - 2 a 8. Z ostatních buněk můžeme tedy dvojku a osmičku také zrušit.

Zrušením dvojky a osmičky získáme ve druhé buňce jediného kandidáta - číslici 1 a proto můžeme použít techniku Naked Single a jedničku do buňky zapsat. Tím ale nastává situace, kdy můžeme jedničku jako kandidáta zrušit z ostatních buněk řádku. (Mimochodem zde je vidět, že technika Naked Single je v podstatě podmnožinou techniky Naked Subset, podobně jako Naked Pair nebo Triplet …)

Po všech úpravách při několikanásobném použití této techniky vypadá situace dle posledního obrázku. Z původních 29 kandidátů v celém řádku jsme dospěli k 15 a jednu číslici jsme mohli přímo doplnit. Účinná technika.
2.6 Technika Hidden Subset
Podobně jako u Naked Subset pokud se technika týká dvou kandidátů, nazýváme ji Hidden Pair, pokud tří potom Hidden Triplet, popř. Hidden Quad pro čtyři kandidáty.
Tato technika je podobná technice Naked Subset, umožňuje ale eliminaci kandidátů právě v těch buňkách, ve kterých nacházíme jisté pravidlo, zatímco buněk okolo se tato technika nijak nedotkne.
Základní pravidlo by se dalo vyjádřit asi takto - "Pokud se určití kandidáti nacházejí pouze v určitých buňkách jednoho řádku, sloupce nebo bloku, a počet těchto buněk je stejný jako počet oněch kandidátů, můžeme ostatní kandidáty z oněch buněk odstranit."
Možná zase trochu nejasné, ale pro dva kandidáty (a tedy Hidden Pair) platí - "Pokud se dva kandidáti nacházejí pouze ve dvou buňkách řádku, sloupce nebo bloku, pak ostatní kandidáti z těchto dvou buněk mohou být odstraněni." Podobně pro tři kandidáty v Hidden Triplet, atd…

Příklad: V řádku se všemi vypsanými kandidáty můžeme najít trojici číslic 6, 7, 9, kdy se tyto číslice vyskytují pouze ve třech buňkách - čtvrté, šesté a deváté. (To, že v deváté nejsou všechny číslice není podstatné.) Znamená to, že tyto tři číslice obsadí ony tři buňky (nevíme ale která kterou) a proto je možno v oněch buňkách ostatní kandidáty zrušit.

Výsledek můžeme pozorovat na dalším obrázku.
Moje zkušenost je taková, že technika Hidden Subset se aplikuje mnohem hůř než třeba Naked Subset, neboť skupiny kandidátů se mnohem hůř nacházejí (o čemž hovoří už samotný název techniky - hidden (skrytý) na rozdíl od naked (obnažený)).
2.7 Technika X - Wing
Touto technikou dokážeme eliminovat kandidáty v některých buňkách, pokud nastane zvláštní postavení některých kandidátů. Vše vysvětlí příklad s obrázkem.
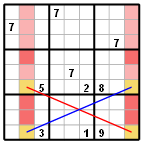
Z obrázku je patrno, že v řádcích 6 a 9 se mohou vyskytovat číslice 7 pouze v polích označených žlutě (čili v obou řádcích pouze ve druhé nebo deváté buňce). Zároveň platí, že číslice 7 patří buď do buněk spojených červenou nebo do buněk spojených modrou čarou (Tyto dvě čáry dávají technice část svého jména - X).
Je tedy zaručeno, že v ostatních buňkách ve sloupcích 2 a 9 se číslice 7 vyskytovat nemůže a proto je možné ze všech růžových buněk sedmičku z kandidátů odstranit. (Ve světle růžových buňkách se sedmička mezi kandidáty nevyskytovala již z jiných důvodů.)
2.8 Technika Swordfish

Podle této techniky platí, že jestliže máme kandidáty jedné číslice ve třech sloupcích / řádcích rozmístěny tak, že jsou v každém sloupci / řádku dva kandidáti a současně platí, že kandidáti z těchto sloupců / řádků jsou vždy dva ve stejném řádku / sloupci (nepočítaje kandidáty z dalších sloupců / řádků), pak je možné z daných řádků / sloupců kandidáty stejného čísla z ostatních buněk odstranit. Předpokládám, že z této věty nezmoudří asi nikdo, proto rovnou příklad. A dáme si kompletní sudoku tabulku.
Do tabulky s doplněnými některými číslicemi jsou vepsáni i všichni kandidáti.
Nejprve použijeme dříve vysvětlené techniky pro eliminaci některých z nich. Konkrétně použijeme techniku Naked Subset v prvním bloku, kde ji použijeme pro eliminaci kandidátů 2 a 6.
Dále použijeme tutéž techniku ve čtvrtém bloku pro eliminaci kandidátů 4 a 6.
No a do třetice je možno stejnou technikou (tentokrát Naked Triplet) eliminovat v pátém bloku kandidáty 4, 6 a 7 - tedy odstranit z první buňky čtyřku a šestku.
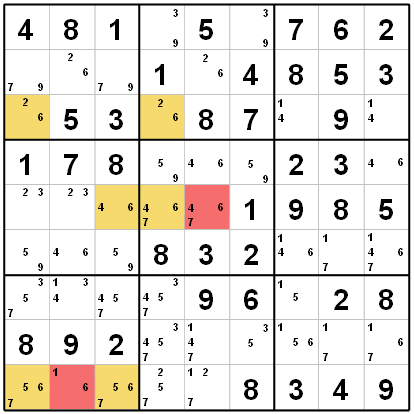
Po těchto úpravách je tabulka zjednodušena viz další obrázek.
A zde dochází k situaci, na kterou jde použít techniku Swordfish.
V prvním, třetím a čtvrtém sloupci kandiduje šestka vždy ve dvou buňkách a to tak, že jsou tyto buňky rozmístěny po dvou i ve třech řádcích (konkrétně ve třetím, pátém a devátém). Buňky jsou označeny žlutě.
Podle pravidla této techniky pak můžeme odstranit všechny ostatní kandidáty číslice 6 z dalších buněk těchto řádků, tedy z těch, které jsou vyznačeny růžově.
Tato technika je vlastně rozšířením techniky X - Wing, popř. opačně - technika X - Wing je zjednodušený případ techniky Swordfish.
2.9 Technika XY - Wing
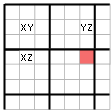
Tato technika může eliminovat kandidáta z jedné nebo i více buněk při určitých podmínkách viz příklad.
Na prvním obrázku je první z možných situací. V buňkách jsou zapsáni všichni kandidáti buněk. Pokud v buňce v prvním bloku má být X, potom v buňce ve čtvrtém bloku musí být Z a tak můžeme v pátém bloku v růžové buňce Z eliminovat. Pokud ale v prvním bloku má být Y, ve druhém bloku bude Z a proto v pátém bloku můžeme z růžové buňky eliminovat opět Z. Čili při tomto rozložení kandidátů je jasné, že v růžové buňce se nemůže nikdy nacházet Z.
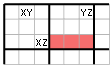
Situace může ale vypadat i jinak. Na dalším obrázku je podobná situace, odehrávající se nyní pouze ve dvou blocích. Je zajímavé, že v této situaci můžeme eliminovat Z ze všech tří růžových buněk ve druhém bloku.
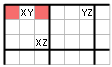
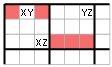
Pozor ale, v této situaci je možné eliminovat Z ještě z dalších dvou buněk ležících v prvním bloku, jak je naznačeno na dalším obrázku. Celá situace se pak dá vyjádřit obrázkem vpravo. Ze všech růžových buněk můžeme eliminovat Z.
2.10 Technika XYZ - Wing
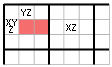
Je variantou techniky XY - Wing. Při rozložení dle prvního obrázku můžeme z růžově označených buněk eliminovat Z, neboť pokud je ve čtvrté buňce prvního bloku X, potom v páté buňce druhého bloku musí být Z a tím je Z vyloučeno ze zbytku druhého řádku. Pokud je ve čtvrté buňce prvního bloku Y, potom musí být ve druhé buňce prvního bloku Z a tím je z ostatních buněk prvního bloku Z vyloučeno. No a jestliže je ve čtvrté buňce prvního bloku Z, nemůže být Z v žádné jiné buňce prvního bloku.
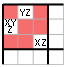
Podobně jako u techniky XY - Wing i zde existuje jiná varianta, která se dá zobrazit v jediném bloku viz druhý obrázek. Zde jde ve všech růžových buňkách eliminovat Z, navíc však i X a Y, k tomu jsme však mohli využít již dříve popsanou techniku Naked Subset, konkrétně zde Naked Triplet.
2.11 Technika Colouring (obarvování)
Tato technika je vhodná pro eliminaci kandidátů určité číslice při využití řádků, sloupců a bloků, které vždy obsahují pouze dva kandidáty oné číslice.
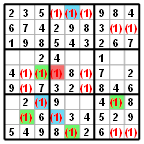
V ukázce je vidět situace, při které se zajímáme o kandidáty číslice 1. Tito kandidáti jsou zobrazeni červeně v závorce, kandidáti ostatních číslic nejsou zobrazeni vůbec, nejsou pro náš příklad potřební.
V tabulce je (střídavě) zelenou a modrou barvou označen tzv. řetězec kandidátů jedničky tam, kde existují pouze dva v jednom řádku, sloupci nebo bloku. Protože musí být jeden z nich nakonec do buňky zapsán a zároveň druhý z nich ne, je jasné, že buď budou jedničky na místě modrých buněk nebo na místě zelených buněk.
Ať už tomu bude tak nebo tak, můžeme eliminovat kandidáta jedničky v buňce označené růžově.
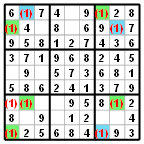
V dalším příkladě vznikne jiná situace, kdy po "colouringu" - obarvení buněk podle pravidel obarvování (tam, kde jsou pouze dva kandidáti v řádku, sloupci nebo bloku) dojde k tomu, že v sedmém bloku se vyskytují dvě buňky obarvené stejně.
Protože ale nemohou být v tomto bloku dvě jedničky, je jasné, že musejí být jedničky v modrých buňkách, zatímco ze zelených je možné jedničky eliminovat. V sedmém bloku bude nakonec jednička v první, nevybarvené buňce.
Pozn.: I když má tato metoda jistě své obrovské výhody, při vlastním praktickém luštění sudoku hlavolamu je použitelná obtížně. Pokud bychom ji totiž chtěli při luštění na papíře použít pro eliminaci i dalších číslic, potřebovali bychom více barviček, což by vedlo zejména k nepřehlednosti situace. Nemluvě o tom, že při luštění on-line tato metoda prostě použít nejde.
2.12 Technika Remote Pairs
Technika kombinuje dříve vysvětlené techniky Naked Subset (konkrétně Naked Pairs) a Colouring.
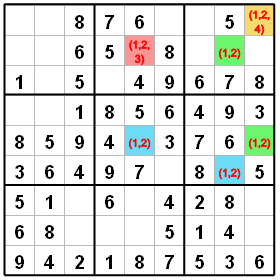
V příkladu jsou podobně jako u Colouringu obarveny buňky, které obsahují stejné páry kandidátů (v tomto případě jsou v buňkách vypsáni vždy všichni kandidáti buněk, ne jen vybraní). Platí obdobně jako u Colouringu, že číslice 1 může být buď v zelených nebo modrých buňkách. Platí také, že dvojka musí být potom v modrých nebo zelených (čili těch "zbývajících") buňkách. Ať už tak nebo tak, můžeme z růžové buňky jedničku i dvojku eliminovat.
Pozor, pomůcka: Počet obarvených členů řetězce včetně prvního a posledního (těch, které rozhodují o eliminaci v některé buňce) musí být sudý (nebo-li krajní členy musejí mít různou barvu), v našem případě R2C8 - R6C8 - R5C9 - R5C5.
Jak je vidět z příkladu - ve žluté buňce v prvním řádku a devátém sloupci nemůžeme eliminovat nic proto, že řetězec buněk R2C8 - R6C8 - R5C9 má jen tři členy (čili lichý počet).
2.13 Technika XY Chains
Touto technikou můžeme eliminovat kandidáty, pokud vznikne řetězec složený dvojic kandidátů, kde vždy článek řetězce obsahuje jednoho stejného kandidáta jako sousední článek a zároveň řetězec začíná i končí stejným kandidátem.
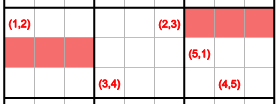
V příkladu máme konstrukci s pětičlánkovým řetězcem (1,2) - (2,3) - (3,4) - (4,5) - (5,1), který umožňuje eliminaci číslice 1 z růžových buněk. Pokud by totiž byla v první buňce dvojka, bude v další trojka, atd … a v poslední buňce řetězce bude jednička. Pokud by to nebylo takhle, byla by přímo v první buňce jednička. V každém případě by ale byla uvedená eliminace možná.
2.14 Technika Forcing Chains
Tato technika se jeví být podobnou technice XY Chains. Můžeme pomocí ní doplnit některé dosud nejisté buňky. Vše nejlépe ukáže příklad.
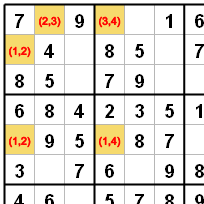
V ukázce vedou od buňky R1C2 k buňce R5C1 dva řetězce. První je R1C2 - R2C1 - R5C1. Druhý R1C2 - R1C4 - R5C4 - R5C1. Řetězce samozřejmě obsahují všechny kandidáty buněk.
Pokud bude v buňce R1C2 dvojka, pak bude v buňce R2C1 jednička a v R5C1 dvojka.
Pokud bude v buňce R1C2 trojka, bude v R1C4 čtyřka, v R5C4 bude jednička a v R5C1 dvojka.
V obou případech tedy bude v R5C1 dvojka.
Mimochodem v příkladu na obrázku můžeme chápat řetězce také jinak - první pouze dvoučlánkový R1C2 - R2C1, druhý potom R1C2 - R1C4 - R5C4 - R5C1 - R5C1.
Proto také můžeme stanovit, že v buňce R2C1 bude jednička.
2.15 Technika Trial And Error (Pokus - omyl)
Ačkoliv by se mohlo zdát, že tohle není žádná technika, a snaha o její použití může vzbuzovat úsměv, je to technika zcela regulérní a mnohdy vysoce účinná.
Předchozí metody je někdy obtížné aplikovat, protože bývá problém vhodné buňky v nepřehledné tabulce nalézt. Naopak tato technika se dá aplikovat jednodušeji.
Samozřejmě, že tato metoda nespočívá v tom, že začneme vyplňovat prázdné buňky bez rozmyšlení nějakými číslicemi. Po uvážení vybereme jednoho z kandidátů, doplníme jej do buňky a pokračujeme v luštění hlavolamu kterýmikoliv z již popsaných technik. Pokud dojdeme k tomu, že v hlavolamu nastane chyba (neřešitelná situace), vrátíme se zpět do stavu před použitím techniky Trial And Error a můžeme původně vybraného kandidáta eliminovat.
2.16 Technika Nishio
Tato technika je speciální formou techniky Trial And Error.
Pro kandidáta buňky si položíme otázku, zda by doplněním této číslice do oné buňky bylo znemožněno doplnit i ostatní stejné číslice do buněk tak, aby to odpovídalo pravidlům. Pokud na takovou otázku existuje odpověď kladná (tedy, že doplněním onoho kandidáta do buňky by bylo znemožněno doplnit ostatní číslice do buněk tak, aby to odpovídalo pravidlům), můžeme onoho kandidáta odstranit.